引入
定义
首先我们先看看什么是二叉树的中序遍历?
二叉树的中序遍历即见名知意,对于每个节点,先遍历左叶子节点,再遍历当前节点,最后遍历右叶子节点
举例说明
如图所求:
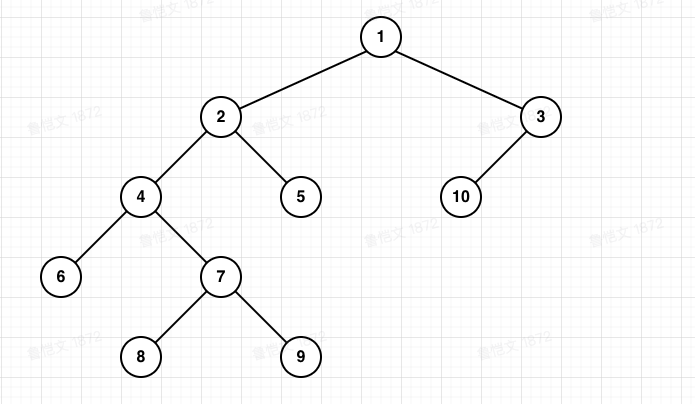
套用上述定义我们轻易到得这棵二叉树的中序遍历结果为:6、4、8、7、9、2、5、1、10、3
解释:
- 我们先来到根节点1,按照定义,先遍历左叶子节点
- 此时我们来到节点2,按照定义,先遍历左叶子节点
- 我们再来到节点4,按照定义,先遍历左叶子节点
- 我们再来到节点6,按照定义,先遍历左叶子节点,由于该节点的左叶子节点为空或者可以理解为没有左叶子节点,所以按照定义的第二步,遍历当前节点,该节点值为6,此时输出
6,再按照定义的第3步,遍历右叶子节点,但右叶子节点为空或者可以理解为没有右叶子节点,所以该节点遍历完成 - 而对于节点6的父节点4来说,此时等同于节点4的左叶子节点遍历完成,所以按照定义的第二步,遍历当前节点,该节点值为4,此时再输出
4,再按照定义的第3步,遍历右叶子节点 - 我们来到了节点4的右叶子节点7,对于节点7按照定义,先遍历左叶子节点
- 我们来到节点8,按照定义,先遍历左叶子节点,由于该节点的左叶子节点为空或者可以理解为没有左叶子节点,所以按照定义的第二步,遍历当前节点,该节点值为8,此时输出
8,再按照定义的第3步,遍历右叶子节点,但右叶子节点为空或者可以理解为没有右叶子节点,所以该节点遍历完成 - 对于8的父节点7而言,此时等同于节点7的左叶子节点遍历完成,所以按照定义的第二步,遍历当前节点,该节点值为7,此时输出
7,再按照定义的第3步,遍历右叶子节点 - 我们来到节点9,按照定义,先遍历左叶子节点,由于该节点的左叶子节点为空或者可以理解为没有左叶子节点,所以按照定义的第二步,遍历当前节点,该节点值为9,此时输出
9,再按照定义的第3步,遍历右叶子节点,但右叶子节点为空或者可以理解为没有右叶子节点,所以该节点遍历完成 - 对于节点9的父节点7来说,右叶子节点遍历完成,按照定义,节点7遍历完成
- 对于节点7的父节点4来说,右叶子节点遍历完成,按照定义,节点4遍历完成
- 对于节点4的父节点2来说,此时等同于节点2的左叶子节点遍历完成,所以按照定义的第二步,遍历当前节点,该节点值为2,此时输出
2,再按照定义的第3步,遍历右叶子节点 - 我们来到节点5,按照定义,先遍历左叶子节点,由于该节点的左叶子节点为空或者可以理解为没有左叶子节点,所以按照定义的第二步,遍历当前节点,该节点值为5,此时输出
5,再按照定义的第3步,遍历右叶子节点,但右叶子节点为空或者可以理解为没有右叶子节点,所以该节点遍历完成 - 对于节点5的父节点2来说,右叶子节点遍历完成,按照定义,节点2遍历完成,
- 对于节点2的父节点1来说,此时等同于节点1的左叶子节点遍历完成,所以按照定义的第二步,遍历当前节点,该节点值为1,此时输出
1,再按照定义的第3步,遍历右叶子节点 - 我们来到节点3,按照定义,先遍历左叶子节点
- 我们来到节点10,按照定义,先遍历左叶子节点,由于该节点的左叶子节点为空或者可以理解为没有左叶子节点,所以按照定义的第二步,遍历当前节点,该节点值为10,此时输出
10,再按照定义的第3步,遍历右叶子节点,但右叶子节点为空或者可以理解为没有右叶子节点,所以该节点遍历完成 - 对于节点10的父节点3来说,此时等同于节点3的左叶子节点遍历完成,所以按照定义的第二步,遍历当前节点,该节点值为3,此时输出
3,再按照定义的第3步,遍历右叶子节点,但右叶子节点为空或者可以理解为没有右叶子节点,所以该节点遍历完成 - 对于节点3的父节点1来说,右叶子节点遍历完成,按照定义,节点1遍历完成
- 到此,这棵二叉树遍历完成
递归遍历
思路
首先我们按照定义“对于每个节点,先遍历左叶子节点,再遍历当前节点,最后遍历右叶子节点”,我们不难发现,对每个节点都有相同的操作,此时就很容易想到递归算法了
Q:有了递归之后就应该去思考递归的终止条件是什么?
A:对于每个节点都有相同的操作,那如果当前节点为空呢?比如上图中的节点6的左叶子节点,遍历到该节点了,它自己都为空或是说这个节点都不存在,也就没有必要继续遍历其叶子节点了,所以我们递归的终止条件就为当前节点不为空
Q:如何递归调用呢?
A:我们按照定义,当进入递归后先要遍历左叶子节点,而遍历左叶子节点与遍历当前节点的逻辑一样,所以直接对左叶子节点递归调用当前方法;遍历完左叶子节点,我们就要遍历(假设我们的遍历操作就是打印出来)当前节点了,我们直接打印当前节点值,接下来要遍历右叶子节点,而遍历右叶子节点与遍历当前节点的逻辑一样,所以直接对右叶子节点递归调用当前方法
代码实现
/**
* 我们就按照力扣上的二叉树的定义来定义二叉树
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public void inorder(TreeNode root) {
//当前节点为空或是说当前节点都不存在,也就没有必要继续遍历其叶子节点了
if (root == null) return;
//遍历左叶子节点
inorder(root.left);
//遍历当前节点
System.out.print(root.val + "\t");
//遍历右叶子节点
inorder(root.right);
}非递归遍历
思路
首先我们先来到节点1,中序遍历的话就是要先遍历左叶子节点,我们来到节点2,同理到节点4、节点6,我们发现对于左叶子节点我们访问的顺序是1、2、4、6,而最后的输出顺序为6、4、2、1,细心的朋友是不是已经发现什么了?先进后出,我们很容易就能想到栈
现在我们初步先使用栈做为容器对根节点的左叶子节点进行压栈操作,直到左叶子节点为空,我们压栈数据依次为1、2、4、6,那么我们弹栈操作就等于是遍历,节点6先出栈,接着节点4出栈,此时我们不能直接继续出栈,因为我们是中序遍历,我们遍历完当前节点后需要遍历其右叶子节点
对于节点4的右叶子节点7而言,我们可以将其看作是一棵二叉树,所以从节点7开始对左叶子节点进行压栈操作,直到左叶子节点为空,此时我们压栈数据为7、8,此时栈内数据按压栈顺序依次为1、2、7、8,再次进行弹栈操作,节点8先出栈,节点7出栈,此时又不能直接继续出栈,因为节点7有右叶子节点
重复上述操作直到遍历完所有节点
我们可以很容易发现不用递归的话我信可以用栈来帮助我们完成这项操作,从根节点开始遍历其左叶子节点,直到左叶子节点为空,出栈,若有右叶子节点则继续重复压栈操作,反之继续出栈,直到栈为空完成遍历
代码实现
public static void inorderTraversal(TreeNode root) {
if (root == null) return;
TreeNode node = root;
Stack<TreeNode> stack = new Stack<>();
while (!stack.isEmpty() || node != null) {
while (node != null) {
stack.push(node);
node = node.left;
}
node = stack.pop();
System.out.print(node.val + ", ");
if (node.right != null)
node = node.right;
else
node = null;
}
}执行结果
我们运行一下代码,得到如下结果
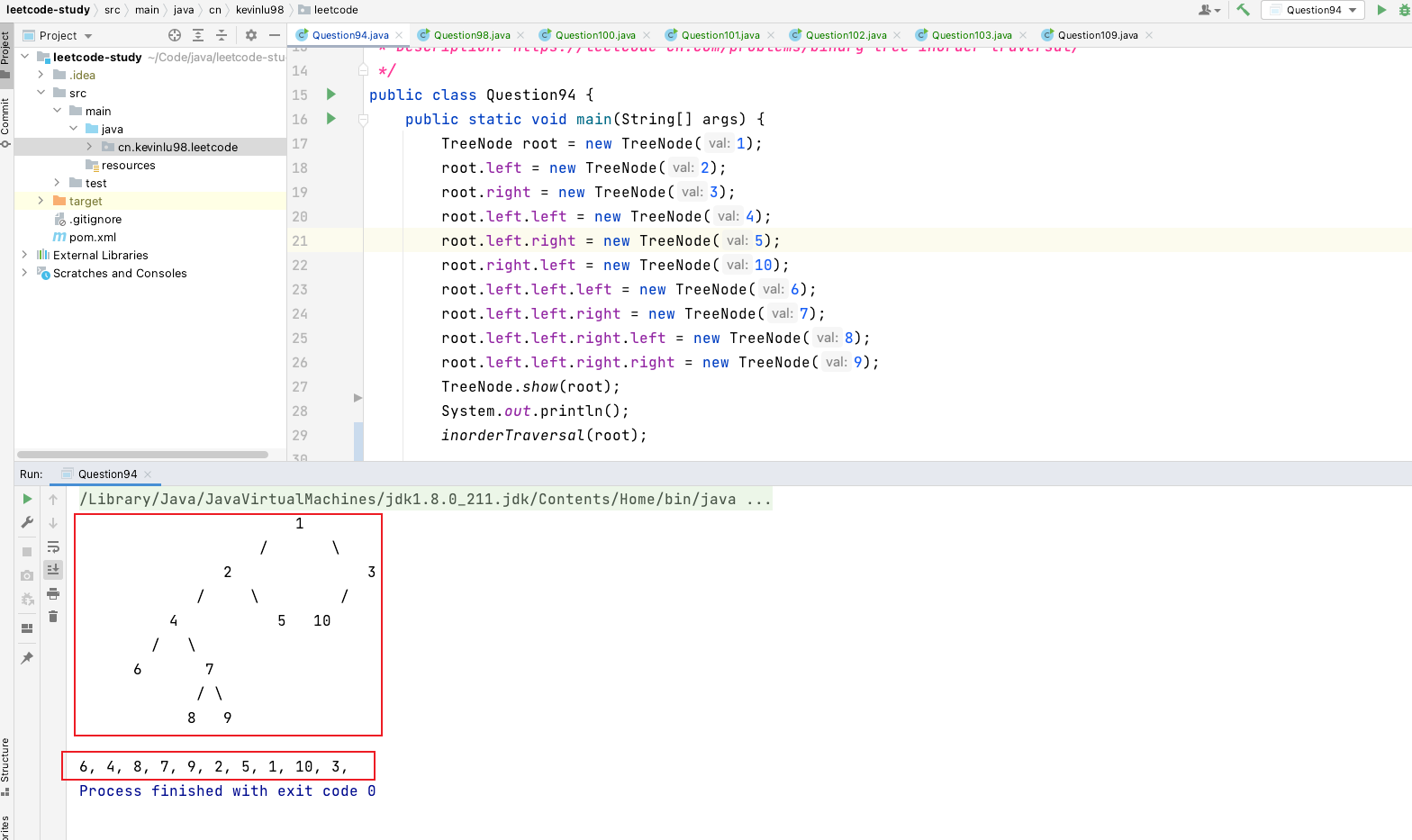



你好这个主题右侧部分在哪设置啊 还是说就是固定这样的?谢谢
不错不错
好耶
看上去真不错
我喜欢, 这里分享真实经验。你的项目 就是 最好的例子。请继续。